Peter Schüller, HTBLuVA Mödling

Zum Inhalt des Artikels

"Computeralgebrasysteme im Mathematikunterricht" - ein zentrales Thema der jüngsten Zeit, das allen am Herzen liegt, Befürwortern wie Gegnern. Doch viele Kollegen scheuen dieses Thema, weil Diskussionen von Spezialisten sehr oft emotionell geführt werden und es ihnen so nicht möglich ist, sich einen realen Überblick zu verschaffen, der ein sachliches Urteil zuläßt.

Dieser Artikel weitet den Begriff "Computeralgebrasysteme" auf "Algebrafähige Rechenhilfen" aus (es sollen auch numerisch orientierte Programme mit algebraischen Fähigkeiten und algebrataugliche Taschenrechner einbezogen werden) und setzt sich zwei Ziele. Zum einen soll aufgezeigt werden, in welchen Bereichen des Unterrichts und unter welchem Aufwand algebrafähige Rechenhilfen in der derzeitigen Form eingesetzt werden können, es soll also der reale Stellenwert solcher Programme aus unterrichtlicher Sicht herausgearbeitet werden. Zum zweiten wird eine wertende Gegenüberstellung unterschiedlicher Systeme (an Hand der bekanntesten Vertreter) versucht. Die Wertung erfolgt dabei ausschließlich in Hinsicht auf eine Eignung für den Unterricht. Dieser Teil schließt den Versuch ein, jedem Kollegen eine individuelle Entscheidungshilfe für seinen persönlichen Gebrauch und Unterricht zur Verfügung zu stellen.

1. Von "Computeralgebrasystemen" zu "Algebrafähigen Rechenhilfen"

1.1 Zum Thema Leistung von Computeralgebrasystemen

Computeralgebrasysteme sind zu einem festen Begriff geworden und aus schulischer Sicht im Mittelpunkt des Interesses. Bei Diskussionen, welches Programm für einen Einsatz in der Schule "besser" sei, wird in der Regel sehr schnell die Leistung des jeweils bevorzugten Produktes in den Vordergrund gestellt. In oft emotionell geführten Gesprächen wird aufgezählt, "was das eine Produkt alles bietet und was auf anderer Seite fehlt". Dazu wäre zu vermerken, daß Computeralgebrasysteme als Arbeitswerkzeuge für den wissenschaftlichen Bereich entwickelt worden sind und somit hinsichtlich ihrer mathematischen Leistung den Bedarf eines Schulunterrichtes von vornherein nicht nur abdecken, sondern ihn um Dimensionen überragen.
 
 

Anmerkung:  Der Leistungsumfang von Computeralgebrasystemen reicht prinzipiell weit über die Bedürfnisse des schulischen Unterrichts hinaus.

Überlegungen bezüglich Eignung für einen Einsatz im schulischen Umfeld müssen deshalb stets aus anderer Sicht angestellt werden. Es ist notwendig gezielt Bereiche zu hinterfragen, wie etwa die Erlernbarkeit eines Produktes, die Übersicht und Lesbarkeit der Bildschirmausgabe, oder die Toleranz und Reaktion bei Eingabefehlern. Es sind also für den schulischen Einsatz andere Merkmale maßgebend als die absolute algebraische Leistung (im Abschnitt 5.2 wird versucht, dies ausführlich zu besprechen und darzulegen).

1.2 Der Begriff "Algebrafähige Rechenhilfen"

Mir erscheint es wichtig, denkt man über zukünftige Formen des Mathematikunterrichtes nach, sich nicht lediglich auf Computeralgebrasysteme zu konzentrieren, sondern ein weiteres Feld einzubeziehen. Es gibt eine Reihe von Rechenhilfen, die vordergründig andere Aufgaben zu erfüllen haben, jedoch ebenfalls mit algebraischen Fähigkeiten ausgestattet sind. Es seien hier konkret zwei Beispiele angeführt:

Zum ersten das Softwareprodukt MathCad der Firma MathSoft Inc., das numerische Berechnungen in den Mittelpunkt des Konzeptes stellt, jedoch zusätzlich mit einem algebraischen Symbolprozessor (Maple) ausgestattet ist, dessen Leistungsumfang für den schulischen Bereich bei weitem ausreichend scheint.

Zum anderen dürfen auch Taschenrechner der jüngsten Generation, wie etwa die Modelle der Serie 48 der Firma Hewlett Packard, nicht außer acht gelassen werden. Sie sind ebenfalls primär numerisch orientiert, bieten aber bereits eine Unzahl an Möglichkeiten, die einem CAS bereits heute sehr nahe kommen (symbolisches Differenzieren und Integrieren, 2D und 3D Graphiken, Darstellung von Richtungsfeldern....). Durch ihre prinzipiellen Vorteile wie Handlichkeit und Unabhängigkeit von jeder Stromversorgung sind sie gerade im technischen Schulbereich in alle Überlegungen einzubeziehen.

Aus diesen Gründen schien mir für vergleichende Untersuchungen das Feld mit dem Begriff Computeralgebrasysteme doch zu eng gesteckt. Ich habe deshalb den Bereich um die oben angeführten Rechenhilfen erweitert und unter dem neuen Oberbegriff Algebrafähige Rechenhilfen zusammengefaßt

2. Einteilung der algebrafähigen Rechenhilfen nach Anwendungszielen
     (inhaltliche Komponenten)

Um eine spätere Beurteilung zu ermöglichen, soll vorerst eine Einteilung der algebrafähige Rechenhilfen erfolgen, die sich an der Form ihres Einsatzes orientiert.

2.1 Algebrafähige Rechenhilfen als Arbeitswerkzeug (Tool)

Bei Diskussion wird fast immer dieser Punkt vordringlich gesehen und angesprochen, er soll deshalb auch gleich an erster Stelle angeführt und behandelt werden. Gemeint dabei ist der Einsatz als reine Arbeitshilfe, also als Werkzeug zum Bewältigen konkreter mathematischer Probleme.

Fortschritte

• Bisher unterlagen Problemstellungen in jedem Detailschritt der Notwendigkeit der unmittelbaren symbolischen und numerischen Lösbarkeit durch den Schüler. Bei Einsatz algebrafähiger Rechenhilfen besteht nun endlich die Möglichkeit, sich von solchen Einschränkungen zu lösen.
• In der Folge kann der Unterricht frei werden für echte Anwendungen. Waren bisher die Anwendungsaufgaben des Mathematikunterrichtes zum überwiegenden Teil Mathematikbeispiele, denen gewissermaßen "ein anwendungsorientiertes Mäntelchen" umgehängt wurde, so wird es nun möglich, echte Aufgabenstellungen zu rechnen.
• Der Reiz des Arbeitens mit einem solchen Medium ist a priori bei den Schülern auf jeden Fall gegeben, und sei es nur wegen der (natürlich falschen) Hoffnung, daß ihnen das Medium Denkarbeit abnimmt.
• Die graphische Unterstützung, die ein solches Medium zur Verfügung stellt, gestattet einen völlig anderen Bezug zur eigentlichen Problemstellung und erweitert die Möglichkeiten der Lösungsansätze beträchtlich.
• Die "mechanische" Rechenarbeit bleibt dem Rechner überlassen, somit werden die Arbeiten weitgehend frei von reinen Rechenfehlern. Die inhaltliche Komponente tritt beim Lösen von Aufgaben in den Mittelpunkt.

• Ein zentrales Problem stellt die mangelnde Übersicht dar. Bereits nicht allzu umfangreiche Aufgabenstellungen erfordern beim Lösen wiederholtes Bildschirmblättern. Selbst das Öffnen mehrerer Fenster kann dieses Problem nicht befriedigend lösen.
• Es ist notwendig, gleiche Bedingungen für jeden Schüler schaffen. Um das Medium als Arbeitswerkzeug voll einsetzen zu können, muß es jedem Schüler im Unterricht, zu Hause und bei der Leistungsfeststellung zur Verfügung stehen.
• Zur Zeit ist der technische Aufwand für eine solche allgemeine Verbreitung im Unterricht noch so gewaltig , daß ein durchgehender Einsatz nicht unmittelbar realisierbar scheint. Die technologische Entwicklung läßt dieses Problem allerdings immer weiter in den Hintergrund treten.
• Der durchgehende Einsatz von Algebrafähigen Rechenhilfen als Arbeitswerkzeug würde die Schwerpunkte von den mathematischen Fertigkeiten klar in Richtung der mathematischen Fähigkeiten verlagern. So wünschens- und anstrebenswert dieser Aspekt auch ist, darf doch nicht vergessen werden, daß so die Anforderungen an die Schüler deutlich steigen und bei unvorsichtiger Handhabung sehr rasch die Gefahr einer Überforderung gegeben wäre!

Vielfach wird vorwiegend in diesem Bereich die Zukunft gesehen und diskutiert. Mit Sicherheit ist aber der Einsatz als Arbeitswerkzeug (Tool) die am schwierigsten und am langsamsten zu installierende Einsatzform. Als einzige der drei aufgezeigten Einsatzformen steckt sie noch in den Kinderschuhen. Zur Zeit sind, abgesehen von Modellversuchen, bestenfalls experimentelle Ansätze möglich. Trotzdem scheint eine intensive Auseinandersetzung mit der Thematik und ein rechtzeitiger Einstieg in die Materie zwingend und notwendig, wird doch der technologische Fortschritt mit Sicherheit in kürzester Zeit ein anderes Umfeld bescheren. Bleibt auch die genaue Form der Realisierung, vor allem in technischer Hinsicht, derzeit noch offen, so lassen sich die inhaltlichen Merkmale, die zukünftige Arbeitswerkzeuge in der Mathematik mit sich bringen werden, bereits ziemlich klar voraussehen.

2.2 algebrafähige Rechenhilfen als Unterrichtshilfe (Tutor)

Algebrafähige Rechenhilfen werden dabei als Demonstrationsobjekt eingesetzt. Der Lehrer demonstriert auf einem Rechner, in der Regel über ein Overheaddisplay. Die Schüler beobachten, arbeiten aber nicht selbst. Die algebrafähige Rechenhilfe dient dabei als Vermittler der Anschauung. So kann der Zugang zu einem tiefergehenden Verständnis erleichtert werden.

Fortschritte

• Algebrafähige Rechenhilfen bieten die Möglichkeit einer (unmittelbaren) Visualisierung des dargebotenen Lehrstoffes in bisher nicht erreichbarer Qualität und Flexibilität.
• Diese Visualisierung ist nun, im Gegensatz zu den klassischen Mitteln wie Overheadfolie oder Film, interaktiv möglich! Einwände oder Vorschläge der Schüler können unmittelbar umgesetzt werden.
• Der Einsatz ist dabei keineswegs auf die Graphik beschränkt. Die Algebrafähigkeit der Produkte sowie ihre überragenden Rechenleistungen (wie etwa im Bereich der Langzahlarithmetik) eröffnen vielfältigste neue pädagogische Möglichkeiten.

• Der Einsatz des Mediums als Tutor verlangt in der Regel nach einer klassenweit einsichtigen Projektion. Dabei treten vielfach noch technische Probleme auf (mangelnde Verdunkelung, Qualität der Overheaddisplays…).
• Die Hardware-Komponente muß zur Zeit noch als aufwendig bezeichnet werden, wenn auch Notebooks in Hinsicht auf Größe und Gewicht bereits klar den Weg der Zukunft aufzeigen.
• Eine Große Gefahr liegt in der Person des Lehrers selbst. Bei guter Vorbereitung und eigener Begeisterung wird das Maß der Aufnahmefähigkeit der Schüler (mehrere Bildschirmseiten, zu rasches Vorgehen) leider sehr, sehr rasch überschritten. Unruhe und "geistiges" Abschalten sind dann die Folge.

In dieser Einsatzform steckt ein ungeheures Potential an neuen Möglichkeiten im methodisch-didaktischen Bereich! Man kann ruhig sagen, daß vielfach neue Dimensionen eröffnet werden. Ein Verzicht auf diesen "Hilfslehrer" bei gegebenen Möglichkeiten und Voraussetzungen würde eher unverständlich scheinen. Weiters kann gesagt werden, daß diese Form eines Einsatzes von algebrafähigen Rechenhilfen bereits heute weitgehend ausgereift ist und kaum mehr echte Bedürfnisse offen läßt. Die Hard- und Software bietet heute faktisch alles, was wünschenswert erscheint.

2.3 Algebrafähige Rechenhilfen als Hilfsmittel zur Erstellung von Unterrichtsmitteln

Die moderne Software der algebrafähigen Rechenhilfen ist durchwegs mit Gestaltungsmöglichkeiten ausgestattet, die vielfach an die Möglichkeiten einer Textverarbeitung heranreichen, ja ihnen manchmal sogar ebenbürtig sind. In Verbindung mit einem Drucker bietet sie somit dem Lehrer die Möglichkeit, Unterrichtsmittel wie etwa Folien, Skripten oder Angaben in kürzerer Zeit in bisher nicht erreichter Qualität herzustellen. Erforderlich hierzu ist ein PC (zu Hause oder in der Schule) und ein Drucker.

Fortschritte

• Die Qualität der heutigen Programme gestattet das Erzeugen optimaler Unterrichtshilfen mit minimalen Aufwand.
• Die Programme gestatten das Erzeugen von Folien oder Skripten mit perfekten Graphiken, Tabellen, Musterberechnungen....
• Der Einsatz der Programme als Korrekturhilfe (Nachrechnen komplexer "Irrwege" von Schülern)
• Das Verfassen von Übungsbeispielen verbindet Aufgabenstellung mit kompletter Kontrollberechnung für den Lehrer
• Das individuelle Variieren der Angaben für jeden Schüler ist ohne großen Mehraufwand möglich
• Mit einigen Produkten ist sogar einfachstes Schreiben von Angaben in höchster Qualität möglich

Bei Erstellung der Unterlagen zu Hause muß die Anschaffung der notwendigen Hardware auf Kosten des Lehrers erfolgen (sofern er diese aus Mathematik-EDV-Interesse nicht ohnehin bereits besitzt)

Bei Erstellung der Unterlagen in der Schule ergibt sich das Problem einer oft mangelnden Vertrautheit des Lehrers mit der Materie, was den Zeitaufwand nicht unerheblich vergrößern kann.

Die beiden "klassischen" Einsatzformen (Tutor und Tool) sind in der Literatur weitverbreitet und auch ausführlich besprochen. Dort aber kaum zu finden, vor allem nicht als eigenständiger und gleichwertiger Punkt, ist der Einsatz als Mittel zur Ausfertigung von Unterrichtsmitteln. Dabei sehe ich gerade darin einen sehr hohen Anreiz für Lehrer, sich näher mit der Materie auseinanderzusetzen und den Einstieg zu wagen. Aus der Sicht eines Unterrichtseinsatzes muß dieser Punkt sicherlich gleichwertig neben die anderen gestellt werden. In der Praxis wird dies leider noch viel zu wenig beachtet und ausgenützt.

Zusammenfassende Aussagen
 
 

Anmerkung :  Für die Unterrichtspraxis ist der Bereich "Algebrafähige Rechenhilfen als Arbeitswerkzeug" zur Zeit noch von untergeordneter Bedeutung! Die anderen Eigenschaften sind viel wichtiger!

 

Anmerkung :  Die Fähigkeiten als Instrument zur Vorbereitung für Lehrer werden noch weitgehend übersehen. Sie sollten aber zunehmend an Bedeutung gewinnen.

 
 

Anmerkung :  Während algebrafähige Rechenhilfen als methodisches Unterrichtsmittel und als Instrument zur Erstellung von Unterlagen bereits beim heutigen Stand der Technik voll einsetzbar sind, stecken die Möglichkeiten, sie als Arbeitswerkzeug einzusetzen, noch in den Kinderschuhen.

3. Einteilung algebrafähiger Rechenhilfen nach Typen (syntaktische Komponenten)

Immer wieder flammen Diskussionen auf, die einzelne Produkte in den Vordergrund stellen. So war auch der ursprüngliche Anlaß für das Entstehen dieses Artikels die Forderung an meine Person, auf einer Didaktiktagung in einem Vortrag die Programme Derive und Mathematica vergleichend und wertend gegenüberzustellen.

Setzt man sich nun näher und sachlich mit einem Vergleich auseinander, so erkennt man sehr rasch, daß die Unterschiede grundsätzlicher Natur sind und nichts mit vordergründigen Realisierungen bestimmter Detaillösungen zu tun haben. So habe ich versucht, die derzeit führenden Programme nach ihren grundlegenden Konzepten zu unterscheiden und einzuteilen. Dies ist für eine Wertung letztlich unerläßlich, da sich daraus prinzipielle Unterschiede für die einzelnen Einsatzformen ergeben.

Somit können die nachfolgenden Aussagen im wesentlichen auch für andere Produkte, die hier nicht namentlich angeführt sind, relativ leicht übertragen werden und dort ebenfalls als Orientierungsshilfe dienen.

Die nachstehenden Untersuchungen wurden mit den folgenden, zu dieser Zeit aktuellsten Versionen angestellt:

• Derive Version 2.58
• Mathematica für Windows, Version 2.2
• MathCad für Windows, Version 3.1
• HP 48 G

Menüs und Untermenüs, logisch in Gruppen und Ebenen unterteilt, stellen das zentrale Konzept dieser Familie dar. Die Auswahl einer Operation erfolgt durch Auswahl eines Menüpunktes entweder durch Ansteuern mit Tasten (Derive verfügt noch über keine Maussteuerung) oder durch direkte Eingabe eines (hervorgehobenen) Kennbuchstabens. Die Syntax wird so automatisch in die Kommandozeile übertragen. Die Eingabe erforderlicher Parameter erfolgt dabei mit vorgegebenen Masken. Das Merken umfangreicher Syntax ist somit nicht erforderlich.

3.2 Syntaxorientiert - Mathematica

Hier stellt ein interaktiver Syntaxinterpreter das zentrale Konzept dar. Operationen werden über die Tastatur als Text eingetippt, wobei natürlich ganz genaue Syntaxrestriktionen zu beachten sind (Groß-Klein-Schreibung, Formen der Klammern, Trennzeichen…). Ein Anspringen einer oder gar mehrerer Menüebenen ist somit nicht erforderlich. Als Programm unter Windows steht zwar eine Maus zur Verfügung, ihr Einsatz beschränkt sich jedoch vorwiegend auf die unter Windows üblichen Grundfunktionen (Markieren, Anklicken von Menüpunkten, …). Bekanntester Vertreter ist das amerikanische Programm Mathematica, in weiteres Produkt ähnlicher Konzeption und etwa gleichen Leistungsumfanges ist das kanadische Produkt Maple.

3.3 Numerisch orientiert - MathCad

Das Produkt MathCad hat als zentrales Konzept das freie Arbeiten auf einem Blatt. Wie auf einem Zettel können Formeln, Tabellen, Funktionen, Graphiken, Texte an jeder Stelle des Arbeitsblattes eingegeben und bei Bedarf sogar im Nachhinein beliebig verschoben werden. Das Programm hat, obwohl ursprünglich auch als DOS Version konzipiert, als bisher einziger Vertreter den Umstieg in die Windows-Welt wirklich realisiert. Es bietet somit von der Benutzeroberfläche her eine Übersicht (und einen Komfort), die für die anderen Produkte als beispielgebend bezeichnet werden muß.

Dem numerischen Berechnen von mathematischen Problemen kommt dabei zentrale Bedeutung zu. Man könnte fast von einer (gelungenen) Projektion des Taschenrechners auf den PC sprechen, natürlich unter Ausnutzung aller dort verfügbaren Möglichkeiten. Das Programm verzichtet vordergründig bewußt auf symbolische Operationen. Will man auf die algebraischen Fähigkeiten, über welche das Programm ebenfalls verfügt, zugreifen, so muß man (natürlich nur einmal) erst einen Symbolprozessor laden. Die Algebra steht also hier als eine Art Zusatzprogramm zur Verfügung.

3.4 Taschenrechnerorientiert (HP48G/GX)

Mit der Serie 48 hat die Firma Hewlett Packart einen Taschenrechner geschaffen, der zukunftsweisend scheint und bereits vielfach als Trendsetter fungiert. Er ist in seinen Funktionen zwischen Taschenrechner (Format, Tastenbedienung…), Computer (eigenes Betriebssystem in 512K ROM, eingebaute serielle Schnittstelle mit KERMIT-Protokoll, strukturierte Programmiersprache…) und einem Computeralgebrasystem (Formeldarstellung, Formel-umwandlung, symbolische Analysis, Graphikbildschirm mit 2D und 3D Graphiken…) angesiedelt. Vor allem wegen einer unübertroffenen Handlichkeit bei kaum glaublicher Leistungsvielfalt und einem in Summe minimalen Anschaffungspreis sollte er in Überlegungen betreffend eines Einsatzes im Unterricht unbedingt auch einbezogen werden. Natürlich kann er auch hier lediglich eine Familie vertreten, da Konkurrenzprodukte sicherlich rasch nachziehen werden.

4. Übersichtliche Beschreibung der einzelnen Vertreter

Da nicht alle Leser alle angesprochenen Produkte (Geräte) genauer kennen werden, sei hier eine übersichtliche Kurzbeschreibung angeboten. Die Auswahl der Stärken und Schwächen ist natürlich subjektiv und mit Sicherheit nicht vollständig (was den Rahmen dieses Artikels auch bei weitem sprengen würde). Weiters werden lediglich Merkmale angeführt, die für die Bedürfnisse eines Einsatzes im Unterricht von Bedeutung sind.

4. 1 Mathematica

Stärken

• Die Syntaxrestriktionen sind gewaltig. Es ist eine genaue Unterscheidung der Groß- und Kleinschreibung erforderlich. Da es sich um einen Kommandointerpreter handelt, kommt es wie in einer Programmiersprache auf jedes einzelne Zeichen an (so löscht etwa der Befehl Remove["Global`*"] alle vordefinierten Variablen).
• Das Programm produziert oft eine Unzahl von Fehlermeldungen. Für jedes auftretende Problem wird eine eigene Fehlermeldungen direkt in das Arbeitsblatt geschrieben, was die Übersicht und Verständlichkeit doch sehr stört.
• Die optimalen Gestaltungsmöglichkeiten der Graphen sind nur über detailliertes sytaktisches Eingeben der Optionen möglich, was zB. bei 36 Wahlmöglichkeiten (siehe oben) und exakter Syntax sich als sehr aufwendig erweist und faktisch nur mit Handbuch oder Hilfefunktion möglich ist.
• Die Übersicht und Lesbarkeit kann bezüglich des heutigen Standards nur als dürftig bezeichnet werden.
• Die Formatierung der Ausgabe von Tabellen läßt zu wünschen übrig
• Die Hardware-Anforderungen müssen als gewaltig bezeichnet werden (Prozessor mindestens Intel-386 mit installiertem Coprozessor, mindestens 4 Mb RAM - 8 Mb werden empfohlen - und 14 Mb Platz auf der Festplatte)

Es handelt sich hier um ein Computeralgebrasystem der Oberklasse. Hervorstechend sind neben guten algebraischen Leistungen vor allem die Möglichkeiten auf dem Gebiet der Graphik. Die Lesbarkeit und Übersicht der Arbeitsblätter (sie heißen Notebooks) entspricht dabei aber in keiner Weise den mathematischen Leistungen. Eine letztlich gewöhnungsbedürftige Benutzeroberfläche mit genauesten Syntaxrestriktionen bei mehreren hundert Befehlen und Optionen muß für einen Einsatz im Unterricht doch als eher problematisch betrachtet werden

Kommentar:

Das Programm stellt sicherlich eine Bereicherung für den Eigengebrauch des Lehrers dar (phantastische Graphen für Vorbereitungen, Einsatz als Tutor, gute Rechenleistungen). Für einen Einsatz mit Schülern eher weniger geeignet, da die doch schwierige (wenn auch logische) Syntax bei den Schülern meist auf Ablehnung stößt. Hinzu kommen (derzeit) extreme Hardware-Anforderungen.

4.4.2 Derive

Stärken

• Durch konsequentes Menühandling muß sich der Benutzer (Schüler) nur minimalste Syntaxvorgaben merken
• Die vielfältigen Gestaltungsmöglichkeiten im Graphikbereich sind ebenfalls über Menüpunkte anwählbar
• Ein interaktives Arbeiten mit Fadenkreuz in der Graphik ist möglich und gut gelöst
• Empfindet man die Eingabe über Menüpunkte als zu langsam, so ist für Geübte alternativ auch jederzeit eine rein syntaktische Eingabe in der Kommandozeile möglich
• Das Programm mit dem derzeit sicherlich bestem Preis-Leistungsverhältnis (besonders für Schüler)
• Das Programm setzt minimale Ansprüche an die Hardware. Es läuft auf jedem XT (!!) mit 640 K RAM und findet auf einer 360 K Diskette Platz
• Das Programm ist bereits für Palmtops verfügbar

• Das Editieren von Fehlerhaften früheren Eingaben muß schlichtweg als katastrophal bezeichnet werden. Ein direktes Editieren in einer früheren Zeile ist nicht möglich, lediglich ein Neuschreiben. Frühere Ausdrücke bleiben bestehen, Folgeberechnungen müssen schrittweise nachgeholt werden.
• Die Lesbarkeit (Bildschirmdarstellung) ist im Detail recht gut, aber schlecht in der Übersicht
• Die Formatierung der Ausgabe von Tabellen ist dürftig
• Eine Beschriftung der Graphiken ist nicht möglich. Die (vorgegebene) Minimalbeschriftung bei 3D Graphiken teilweise sogar sinnwidrig.
• Bei "zu langen" Ausdrücken fehlt ein Zeilenumbruch
• Die gesamte Benutzeroberfläche stammt aus der EDV-Steinzeit
• Beim Laden von Dateien erhält der Benutzer keinerlei Listing-Unterstützung (Auswahl aus Dateiliste). Namen müssen auswendig gewußt werden.

Ein Computeralgebrasystem, das trotz seiner minimalen Hardwareanforderungen in Bezug auf Leistung für den Oberstufeneinsatz (und auch noch in höheren Bereichen) kaum Wünsche offen läßt. Aus schulischer Sicht besticht das Programm vor allem durch sein konsequentes Menühandling. Faktisch alle mathematischen Befehle und Funktionen können direkt aus Menüs abgerufen werden (lediglich die Funktionen der speziell orientierten Erweiterungspakete müssen geschrieben werden), der Benutzer braucht sich lediglich die (logische) Ordnung zu merken, wo die einzelnen Befehle zu finden sind. Eine kaum verständliche "Platz-Mimimierungs-Philosophie" (alles paßt auch heute noch auf eine 360 Kb Diskette !?!) bringt einerseits Beschränkungen bei der Leistung mit sich (z.B. fehlende Beschriftung bei Graphen), andrerseits bedingt sie vor allem eine mehr als veraltete Benutzeroberfläche. Editiermöglichkeit, Darstellung auf Bildschirm und Druck erscheinen aus der Computer-Steinzeit.

Kommentare

Das Programm ist wegen seiner Menüsteuerung (leichte Erlernbarkeit) und seinem ansprechenden Preis/Leistungsverhältnisses trotz vieler Schwächen für Unterrichtszwecke sehr interessant.

4.4.3 MathCad

Stärken

Ein Programm mit dem Schwerpunkt numerisches Lösen von mathematischen Problemen. Die algebraischen Fähigkeiten (Maple) sind jedoch für den Oberstufenbereich mehr als ausreichend, sie lassen in diesem Ausbildungsbereich faktisch keine Wünsche offen. Das Programm besticht neben ausgezeichneten Rechenleistungen vor allem durch seine Darstellungsform in wirklich allen Bereichen (mathematische Syntax, Graphik, Tabellen, Text...). Seine 100% Windows-Oberfläche ist wahrscheinlich das Beste, was auf dem Sektor der Mathematiksoftware zur Zeit zu finden ist. Der Großteil der mathematischen Funktionen kann durch anklicken von Menüpunkten oder Buttons direkt eingefügt werden, sodaß der Benützer sich kaum Syntaxvorgaben merken muß.

Kommentar

Das Programm scheint ausgezeichnet für das Arbeiten im Unterricht geeignet (besonders als Tool), ganz besonders empfiehlt es sich für den technischen Schulbereich. Es kann wirklich als praktisches Handwerkzeug bezeichnet werden. Weiters ist es von den gegenübergestellten Programmen jenes mit der besten Eignung für das Erstellen von Folien für den Unterricht. Wegen der doch geringeren Hardware-Anforderungen gegenüber Mathematica läuft es im Gegensatz zu diesem auch auf den Schulnotebooks des BMUK.

4.4.4 algebrafähiger Taschenrechner

Stärken

Es handelt sich um ein reines Arbeitswerkzeug, das auf dem Gebiet der Numerik kaum mehr Wünsche offen läßt, wenn auch Geschwindigkeit, multibelegte Tasten, allgemeine Lesbarkeit usw. das reine "Arbeitsvergnügen" trüben. Die algebraischen Fähigkeiten lassen (derzeit noch) zu wünschen übrig. Dem ist eine extreme Handlichkeit und ein minimaler Gesamtanschaffungspreis gegenüberzustellen. Besondere Eignung für den technischen Bereich.

Kommentar

In Geräten dieser Form liegt (meiner persönlichen Meinung nach) die Zukunft, wenn auch in modifizierter Form. Die Vorteile rascher Verfügbarkeit (nur Einschalten), Stromunabhängigkeit (Batterie) und Handlichkeit (minimaler Platzbedarf) werden die Nachteile wie kleiner Bildschirm und mangelnde Geschwindigkeit für den schulischen Einsatz mit größter Wahrscheinlichkeit aufwiegen, umso mehr, da im Bereich Leistung bereits in naher Zukunft kaum mehr Unterschiede zu erwarten sind.

Geräte, die etwa das Aussehen und die Größe eines heutigen Palmtop aufweisen werden, mit allen Fähigkeiten eines Computeralgebrasystems (im ROM) ausgestattet sind und von Batterien gespeist werden, werden in nicht allzu ferner Zeit auf den Tischen unserer Schüler ihren Einzug halten, die Taschenrechner im Mathematikunterricht ersetzen und als Handwerkzeug das Arbeiten auf dem Papier ergänzen und prägen.

 

Anmerkung : Das Bildschirmblättern wird immer, unabhängig von der gebotenen Leistung, verhindern, daß im schulischen Bereich alleine auf dem Rechner gearbeitet wird, also Papier und Bleistift überflüssig werden. Die Zukunft liegt im nachgeordneten Handwerkzeug, nicht im alleinigen Arbeitsinstrument Die Entwicklung wird in Richtung Algebra-Taschenrechner im Palmtopformat gehen.

5. Die Bewertung

Es soll nun versucht werden, diese doch sehr unterschiedlichen Konzeptionen aus unterrichtlicher Sicht einer Wertung zu unterziehen. Um eine jedoch Wertung durchführen zu können, ist vorerst eine sachliche Grundlage notwendig, auf deren Basis Vergleiche angestellt werden können.

5.1 Die Kriterien der Bewertung

Folgende Punkte wurden vorerst als Grundlage für eine Bewertung festgelegt:
 

Handling Menü, allg. Handling Erlernbarkeit Hilfefunktion Editierbarkeit Syntax-Restriktionen

Leistung Algebrafähigkeit Eignung als Werkzeug Graphik Darstellung am Schirm Druck Graphikanimation

Hardwarekomponente Handlichkeit Preis (absolut) Hardwareaufwand Speichermöglichkeiten

 

Ich habe als ersten Schritt in einer Tabellenkalkulation nachfolgende Tabelle erstellt und Punkte von 0 (min) bis 10 (max) vergeben. In der Tabelle finden sich bewußt keine Summen, da sie ohne Bezug zu Inhalten sinnlos wären. Diese Tabelle wertet allein einzelne Funktionen, spiegelt aber vorläufig keinerlei Gesamtaussage wider!

Die hier vergebenen Punkte entspringen vergleichenden Arbeiten. Zu diesem Zweck wurden eine Reihe von für den HTL-Unterricht typischen Ausfgaben (Gleichungen, Gleichungssysteme, Kurvendiskussion, Taylorreihenentwicklung, Fourierreihenentwicklung, 2D- und 3D-Graphiken) mit allen Produkten durchgerechnet und gegenübergestellt.

5.2 Wertung in Bezug auf Einsatzform

Zwischen der Legende am linken Rand und der Wertetabelle finden Sie noch eine freie Spalte. Ich bin nun daran gegangen, in diese Spalte Faktoren einzutragen, die die Wichtigkeit der einzelnen Bewertungspunkte bezüglich der zu besprechenden Einsatzform widerspiegeln. Ich habe hier ebenfalls Faktoren zwischen 0 (ohne Bedeutung) bis 10 (wichtig) vergeben. In Einzelfällen habe ich auch die Faktoren 12 und sogar 15 vergeben, um die zentrale Bedeutung dieser Funktionen zu werten. Die Faktoren sind von der Software unabhängig, sie beschreiben die Bedeutung der einzelnen Funktionen für die zu besprechende Einsatzform. In der Folge werden in der Tabelle die Punkte mit den Faktoren multipliziert und aufsummiert. Die Summen gestatten letztlich eine Wertung aus der Sicht des Einsatzzweckes.

Die Festlegung der Faktoren nahm sehr viel Zeit in Anspruch, jeder Punkt wurde einzeln überdacht, wobei möglichst alle Argumente in Betracht gezogen wurden. Die Bezugsebene stellt dabei immer das schulische Umfeld dar.

Sollten Ihnen einige Werte auf den ersten Blick nicht ganz einsichtig erscheinen, so versuchen Sie alle Seiten zu sehen und abzuwägen, Sie werden mit größter Wahrscheinlichkeit auf die Gründe stoßen, warum gerade dieser Wert gewählt wurde. Ich möchte dies an einem Beispiel erläutern. So habe ich dem Punkt Preis zweimal den Faktor 10 (wichtig) gegeben, einmal (Tutor) jedoch nur den Wert 5. Der Gedanke: Für die Einsatzform Vorbereitung sind die Kosten im Normalfall durch den Lehrer selbst zu tragen, somit hat der Preis höchste Wichtigkeit. Für die Einsatzform Tool ist die Anschaffung vieler Geräte notwendig, meist sogar durch die Schüler selbst, somit wurde ebenfalls der höchster Faktor vergeben. Für die Einsatzform Tutor jedoch reicht die Anschaffung nur eines Gerätes und dieses sollte von der Schule bezahlt werden. Somit scheint plötzlich der Faktor 5 wiederum relativ hoch. Hier wurde jedoch weiter berücksichtigt, daß die Letztentscheidung für die Beschaffung im Schulrahmen zu sehen ist und diese nur in den seltensten Fällen durch einen Mathematiker getroffen wird. Somit erhält der Preis wiederum mehr Gewicht…

Eine detaillierte Besprechung aller Werte in den Tabellen (sowohl Punkte als auch Faktoren) wäre natürlich sehr interessant, würde jedoch den Artikel mindestens auf die vierfache Länge ausdehnen. Es muß deshalb an dieser Stelle darauf verzichtet werden. Der Artikel ist eine Kurzfassung eines Vortrages, der für 2 Stunden konzipiert ist. In diesem Zeitraum ist es mir natürlich möglich alle Punkte einzeln durchzubesprechen, zu argumentieren und mit mehr als 40 Folien die Aussagen zu erläutern. Für Rückfragen und Diskussionen stehe ich natürlich jederzeit gerne zur Verfügung.

Achtung!

Die Wertungen der Faktoren unterliegen natürlich deutlich einer subjektiven Färbung, spiegeln sie doch wider, welche Bedeutung die einzelne Person jedem einzelnen Punkt in Hinblick auf den beabsichtigten Einsatz zumißt. Hier sollen Sie bitte ihre eigenen Werte eintragen, sind doch dafür keine Kenntnisse der Software notwendig. So kann diese Arbeit für Sie zu einer individuellen Entscheidungshilfe werden. Sie finden die vorbereitete Tabelle auf der Diskette dieser Aussendung unter dem Namen AFRHIMMU.XLS (Format Excel 4).

5.2.1 Algebrafähige Rechenhilfen als Arbeitswerkzeug (Tool)
 

Das Programm MathCad erweist sich im Bereich Arbeitswerkzeug klar als bestgeeignet, wobei seine Vorteile sowohl im Handling als auch in der Rechenleistung (numerische Funktionen, Bildschirmdarstellung) zu Buche schlagen.

Derive weist in seiner Funktion als Arbeitswerkzeug vor allem Schwächen im Bereich Handling auf, der wegen der Menüsteuerung eigentlich für das Programm sprechen sollte. Eine faktisch nicht vorhandene Hilfefunktion und große Probleme im Bereich Editieren machen diese Vorteile allerdings wieder zunichte.

Bei Mathematica schlagen sich in seiner Funktion als Arbeitswerkzeug für den schulischen Bereich die schwierige Syntax und in der Folge das allgemeine Handling nieder. Weiters spricht die aufwendige Hardware (zur Zeit noch) gegen das Programm. Die hohen Qualitäten im Bereich Algebra haben im schulischen Umfeld natürlich weniger Bedeutung.

Interessant, aber doch kaum überraschend, ist die hohe Punkteanzahl des "Super-TR", der vor allem seine Vorteile im Bereich Hardware (Handlichkeit, Preis) hat, die bei einem Einsatz als Rechenhilfe im Unterricht natürlich sehr schwer als Argument wiegen.

5.2.2 Algebrafähige Rechenhilfen als Unterrichtshilfe (Tutor)

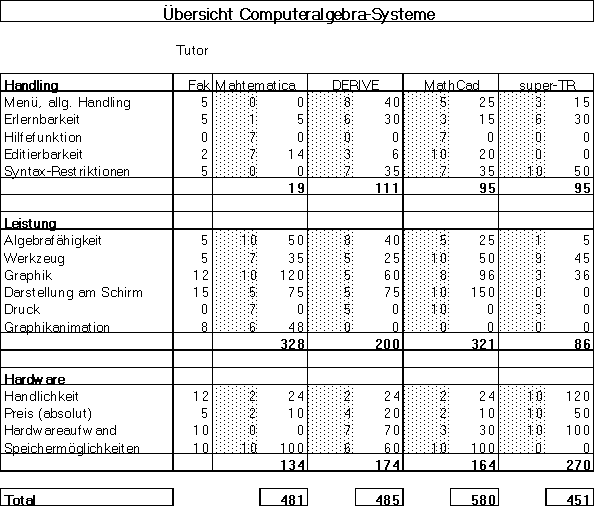
Das Programm MathCad weist im Bereich Verständnishilfe (Tutor) ebenfalls die höchste Punkteanzahl auf, was doch etwas überrascht. Bei etwa gleichmäßig gut verteilter Eignung in allen Bereichen hat die exzellente Bildschirmdarstellung des Arbeitsblattes letztlich doch für ein klares Übergewicht des Programmes gesorgt.

Derive weist in seiner Funktion als Verständnishilfe (Tutor) vor allem Schwächen im Bereich Leistung auf. Mangelnde Graphikdarstellung (Beschriftung!…) und unübersichtliche Bildschirmdarstellung sprechen in diesem Bereich vorerst gegen dieses Programm. Es muß jedoch beachtet werden, daß es im Bereich Hardware voran liegt. Es ist auf jedem PC, insbesondere auf den Notebooks des BMUK, einsetzbar. Ein unmittelbarer Einsatz als Tutor ist somit mit dem geringsten Aufwand zu realisieren.

Der Bereich Verständnishilfe (Tutor) schien auf den ersten Blick die Domäne von Mathematica zu sein. Merkmale wie ausgezeichnete Graphik und sogar die Möglichkeit der Animation ließen hier die Besteignung erwarten. Der Bereich Leistung bringt dies auch mehr als klar zum Ausdruck. In einer Gesamtbeurteilung fällt aber natürlich das Problem der komplizierten Syntax (interaktives Eingeben vor der Klasse von nicht vorbereiteten Schülerfragen) und besonders die Hardwareanforderungen ins Gewicht. Wer allerdings die entsprechende Ausstattung zur Verfügung hat, findet in diesem Produkt nach einiger Zeit des Einarbeitens sicherlich die meisten Möglichkeiten.

Der "Super-TR" sollte hier eigentlich aus der Wertung genommen werden, er ist von vornherein nicht als Verständnishilfe (Tutor) konzipiert. Er rangiert in der Realität noch viel weiter hinter den PC-Programmen, als es durch die Punktezahl im ersten Moment zum Ausdruck kommt. Er sammelt Punkte alleine im Bereich Hardware. Betrachtet man die Bereiche Leistung und Handling, so wird die Distanz deutlich. Dennoch sei zu vermerken, daß sich auch mit solchen Geräten in Hinblick auf Verständnishilfe in kleinem Ausmaße einiges realisieren läßt, wenn man keine anderen Mittel zur Verfügung hat.

5.2.3 Algebrafähige Rechenhilfen als Hilfsmittel zur Erstellung von Unterrichtsmitteln

 
Das Programm MathCad erweist sich auch im Bereich Erstellung von Unterrichtsunterlagen als bestgeeignet, wobei es seinen Wertungsvorsprung gegenüber den anderen Programmen faktisch ausschließlich im Bereich Leistung (bezogen auf Erstellung von Unterlagen) verbucht. Dies liegt vor allem an dem einfachen und flexiblen Handling der Windowsoberfläche (Texte und Formeln mit der Maus an beliebige Stelle ziehen…).

Für Derive sprechen in der Funktion zur Erstellung von Unterrichtsunterlagen vordergründig die geringen Harwareanforderungen. Bereits mit einem alten XT und einem Nadeldrucker können brauchbare Ergebnisse erzielt werden. Weiters kommt es mit seiner leichten Erlernbarkeit dem (nicht geübten) Lehrer doch sehr entgegen. Es muß aber klar gesehen werden, daß es im Bereich Leistung in dieser Themenstellung klar abfällt.

Bei Mathematica bietet sich auch bei der Erstellung von Unterrichtsunterlagen das gleiche Bild. Ausgezeichnete Leistung wird durch kompliziertes Handling und große Hardwareanforderungen teilweise wieder kompensiert. Es muß jedoch auf die konkurrenzlosen Graphikfähigkeiten des Produktes verwiesen werden. Wer in seinen Vorbereitungen auf dem Bereich der Graphik (ganz besonders 3D) einmal Besonderes bieten möchte, sollte zu diesem Programm greifen (notfalls bei einem Bekannten).

Der "Super-TR" wurde bewußt aus der Wertung genommen.

5.3 Wertung in Bezug auf Schulform

In gleicher Weise ist nun sogar jederzeit auch eine Wertung in bezug auf eine beliebige Schulform (HTL, AHS, HAK…) möglich. Sie brauchen lediglich die Spalte Fak (Multiplikationsfaktor) durch eigene Werte zu ersetzen, die diesen Schulformen ihrer Ansicht nach entsprechen. Dies sei jedoch der persönlichen Initiative überlassen, da ich mir kein vergleichendes Urteil bezüglich der Notwendigkeiten in anderen Schulformen anmaßen möchte.

5.4 Zur persönlichen Entscheidung

Sie können (und sollen) nun die Werte in der Tabelle individuell nach eigener Sichtweise, nach persönlichen Bedürfnissen und nach individuell vorgegebenen Rahmenbedingungen verändern. So wird es Ihnen vielleicht leichter fallen, im Einzelfall eine Entscheidung zu treffen.

Dazu noch eine abschließende Bemerkung. Sollten Sie die Möglichkeit haben, in der Schule (oder gar zu Hause) über die entsprechende Hard- und Software zu verfügen, so empfehle ich Ihnen, sich nicht auf ein einziges Produkt zu beschränken. Wie Sie sehen können, hat jedes Programm seine Stärken und Schwächen und Sie sind sicherlich gut beraten, wenn Sie unterschiedliche Produkte, den jeweiligen Stärken entsprechend, einsetzen. Haben Sie vor allem keine Angst davor, sich in mehrere Produkte einarbeiten zu müssen. Der Lernaufwand für das zweite Produkt steht in keiner Relation zum ersten Einstieg, das die inhaltlichen Funktionen im wesentlichen gleich sind, lediglich das Handling umgelernt werden muß.

Der vorige Absatz bezieht sich natürlich auf den persönlichen Bedarf. Im Unterricht wäre der überwiegende Teil der Schüler mit dem Einsatz mehrerer Programme, sofern sie damit aktiv arbeiten sollen, sicherlich überfordert.

6. Ausblicke - ein wichtiger Abschluß

Die Welt der Computer gilt heute als Maß aller Dinge in bezug auf Schnellebigkeit. In immer kürzeren Intervallen erreichen uns Neuerscheinungen und Neuentwicklungen. Was eben noch als senationelle Neuerung galt, ist wenige Monate später bereits überholt. Dies betrifft sowohl den Bereich der Soft- als auch jenen der Hardware.

So kann auch dieser Artikel nur eine Momentaufnahme darstellen. Ich habe mich aber bemüht, den Ansatz der Wertung so zu gestalten, daß diese nicht nur undividuell angepaßt, sondern sie auch jederzeit Neuentwicklungen entsprechend aktualisiert werden kann.

Gerade in Hinblick auf den erfolgten Vergleich ist es aber nun besonders interessant, an den Schluß noch einen kleinen Ausblick zu stellen. Von allen besprochenen Produkten sind neue Versionen angekündigt, die in sehr vielen Dingen gerade jene Punkte verbessern sollen, die hier auf der Seite "Schwächen" zu finden sind.

Mathematica kündigt eine "echte" Windows-Version an mit zweidimensionalem In- und Output! Die zeilenorientierte Ein- und Ausgabe wird also der Vergangenheit angehören und einer "graphischen" Oberfläche nach heutigem Standard weichen, die beispielsweise ein nachträgliches Editieren von Grenzen direkt "im Integral" zulassen wird…

Derive spricht bereits seit langem von einer Windows-Version, die nun endgültig im Herbst erscheinen soll. Man darf gespannt sein, welche Verbesserungen gerade in Hinblick auf Handling (Editieren) und Benutzeroberfläche ein solcher Einstieg in die Windowswelt mit sich bringen wird…

MathCad in der Version 5 (die Version 4 wurde nur kurzzeitig und nur in Englisch ausgeliefert und wird in der Version 5 aufgehen) liegt bereits vor, und zwar in zwei Versionen. Die (billigere) Version 5.0 entspricht der alten Version 3.1 mit Verbesserungen vor allem auf dem Sektor der Graphik. Die Version 5.0+ hingegen schließt nun als Symbolprozessor Maple in seinem kompletten (!) Leistungsumfang ein, womit ein Computeralgebrasystem unter der Arbeitsoberfläche von MathCad zur Verfügung steht…

Werden alle Ankündigungen auch wirklich realisiert, so wird die Wahl zwischen den einzelnen Produkten noch schwerer fallen (oder auch leichter sein), weil entscheidende Unterschiede im wertbaren Bereich (Leistung, Handling, Benutzeroberfläche…) sich immer mehr verwischen werden. Die Entscheidungskriterien Preis, Hardwareanforderungen und nicht zuletzt eine gewisse "Produktphilosophie" werden in den Vordergrund treten. Es bleibt allerdings anzuwarten, welche dieser Neuerungen zu welchem Zeitpunkt, in welcher Weise und in welchem Ausmaß auch wirklich realisiert werden …

Sollten sich gravierende Neuerungen ergeben, so ist daran gedacht, in etwa einem Jahr diesem Artikel eine Aktualisierung (Kurzvorstellung und neue Wertung) folgen zu lassen. Sollten Sie in diesem Sinne Beiträge, Kommentare oder Ergänzungen haben, so ersuche ich Sie, diese an mich einzusenden.

7. Literaturliste

Mathematica griffbereit, Version 2, Blachmann Nancy, Verlag Friedrich Vieweg&Sohn, Braunschweig/Wiesbaden 1993.

Das Mathematica Arbeitsbuch,Heinrich E./Janetzko H.D. Verlag Friedrich Vieweg&Sohn, Braunschweig/Wiesbaden 1994.

Mathematik mit DERIVE, Koepf/Ben-Israel/Gilbert, , Verlag Friedrich Vieweg&Sohn, Braunschweig/Wiesbaden 1993.

MathCAD 3.1 für Windows, Weskamp Martin, Addison-Wesley Publishing Company, Bonn- Paris...1993

Mathematica, Kofler Michael, Addison-Wesley Publishing Company, Bonn-Paris...1992

Softwareübersicht über andere CAS, Stegbauer Heinz, Vortragsskriptum Mai 93

Abschließend seien hier die Bezugsquellen für die einzelnen Programme angeführt und die derzeit (Mai 94) gültigen Preise.

Derive
Uni Software Plus, Softwarepark Hagenberg, A-4232 Hagenberg, Tel.: 07236 - 3338
derzeit gültige Version 2.59

Mathematica für Windows
Uni Software Plus, Softwarepark Hagenberg, A-4232 Hagenberg, Tel.: 07236 - 3338
derzeit gültige Version 2.2

Einzellizenz Vollversion (Windows Enhanced)

S 16.965.- (excl.)

Einzellizenzen für Schulen, Lehrer, Schüler: Student Version : S 3.050.- (excl.);
(Die Student Version hat vollen Funktionsumfang, unterstützt allerdings nicht den Koprozessor oder MathLink. Benötigt 5 Mb RAM sowie 7 Mb auf der Festplatte. Für Windows, DOS, Mcintosh erhältlich.) Schullizenzen:

Bei Ankauf von mindestens 10 Lizenzen mit 1 Vollversion und 9 Lizenzrechten
je Lizenz S 3.680.- (excl.)

Einzellizenz

Vollversion S 9.350.- (excl.)

Einzellizenzen für Schulen, Lehrer, Schüler: Student Version : S 1.500.- (excl.);
(Die Student Version hat kleineren Funktionsumfang, weniger Dokumentation. Für DOS/Windows und Mcintosh erhältlich.) Schullizenzen:

Vollversionen; Preisschema nach "Wurzelformel"
2-4 Lizenzen S 18.700.- (excl.) (entspricht 2 Vollversionen)
3-9 Lizenzen S 28.050.- (excl.) (entspricht 3 Vollversionen) u.s.w.

Einzellizenzen

Vollversion 3.1 DM 260.- (excl.)
Vollversion 5.0 DM 356.- (excl.) (Nachfolge 3.1)
Vollversion 5.0+ DM 860.- (excl.) (includiert komplett Maple!)

Schullizenz

Vollversion 3.1 DM 799.- (excl.)
Vollversion 5.0+ DM 4780.- (excl.)