
dann gilt für Höhen bis zu » 100 km bei konstanter Temperatur die barometrische Höhenformel
Peter Weilharter, HTBLuVA Mödling
| Barometrische Höhenformel |
Kurzzusammenfassung:
Lehrplanbezug:Exponentialfunktion
1. Die barometrische Höhenformel2. Jahrgang
Das Eigengewicht der Lufthülle erzeugt in der Luft einen Druck,
der mit zunehmendem Abstand von der Erdoberfläche kleiner wird. In
der Nähe der Erdoberfläche gilt:
Mit je 8 m Höhenunterschied ändert sich der Luftdruck um
je 100 Pa = 1 hPa.
Setzt man eine in den verschiedenen Höhen gleiche Temperatur voraus,
so nimmt der Luftdruck bei zunehmender Höhe nach einer Exponentialfunktion
ab.

dann gilt für Höhen bis zu »
100 km bei konstanter Temperatur die barometrische Höhenformel
![]()
Für p0 = 101,3 kPa , t = 0° C in der ganzen Atmosphäre
und ![]() folgt
aus (1) und mit Hilfe des Ti-92 Plus
folgt
aus (1) und mit Hilfe des Ti-92 Plus
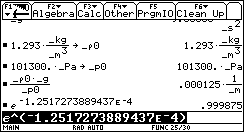
![]()
oder
![]()
2. Herleitung der barometrischen Höhenformel
Aufgrund einer Wertetabelle soll der Schüler erkennen, dass die
Abnahme des Luftdruckes einer Exponentialfunktion folgt.
Folgende Tabelle wurde aus "Ingenieur-Mathematik Band 2 (Timischl/Kaiser)"
entnommen:

Um einen ersten Eindruck von der Kurve, die sich aus obigen Werten ergibt, zu erhalten; werden zunächst die Werte in den Ti-92 Plus eingegeben.
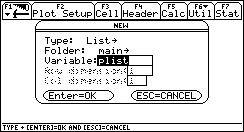
Mit ![]() ® 6 ® 3 bekommt
man folgendes Menü, indem für Type: 3: List wählt und einen
Variablennamen (z.B.: plist) definiert:
® 6 ® 3 bekommt
man folgendes Menü, indem für Type: 3: List wählt und einen
Variablennamen (z.B.: plist) definiert:
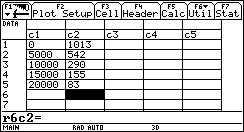
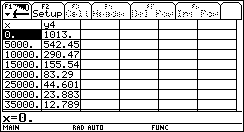
Mit ![]() erhält man eine Tabelle, in der die Werte wie folgt eingetragen werden:
erhält man eine Tabelle, in der die Werte wie folgt eingetragen werden:
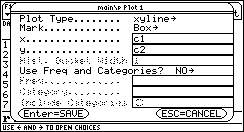
Als nächstes wird ein Graph mit ![]() ®
®![]() ® xyline ®
x = c1 ® y = c2 definiert.
® xyline ®
x = c1 ® y = c2 definiert.
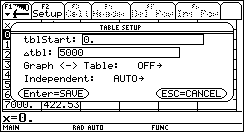
Um ein geeignetes Koordinatensystem zu bekommen müssen die Windowseinstellungen
geändert werden (![]() ®
e ):
®
e ):
Die x-Werte stellen die Höhen dar, die in unserem Beispiel von
0 m bis 20000 m (Skalierung: 5000 m) gehen.
Die y-Werte ergeben den Luftdruck, der bis 1100 mbar (Skalierung: 100
m) geht.
Mit ![]() ® r erhält man folgenden Graphen:
® r erhält man folgenden Graphen:
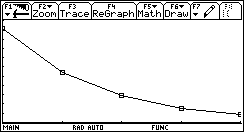
Anhand des Graphen, läßt sich schon eine Exponentialfunktion
vermuten, dennoch gibt es dafür noch keinen Beweis.
Eine wichtige Eigenschaft der Exponentialfunktion liegt darin, dass
bei gleichbleibender Schrittweite D x die relative
Funktionsänderung ![]() konstant ist.
konstant ist.
Es gilt:![]()
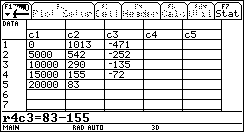
Im Data/Martix-Editor werden die Werte für D
y in der Spalte c3 und in der Spalte c4 die Werte für ![]() berechnet:
berechnet:
 |
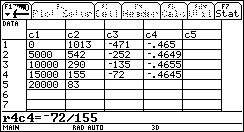 |
Daraus lässt sich leicht erkennen, dass die relative Funktionsänderung
ungefähr den Wert -0,465 annimmt und konstant ist.
Es handelt sich offensichtlich um eine Exponentialgleichung, dessen
Funktionsgleichung nun einfach zu berechnen ist.
Es gilt: ![]() mit
mit ![]() und
und ![]() ergibt
sich:
ergibt
sich:
Diese Gleichung lässt sich normalerweise nur mit Hilfe des Logarithmus lösen, der aber bei der Einführung der Exponentialfunktion und deren Eigenschaften zu diesem Zeitpunkt den Schülern noch nicht bekannt ist.
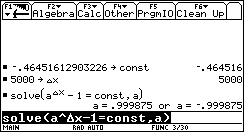
Es werden 2 Lösungen angegeben, wobei die zweite Lösung (negative Basis!) nicht sinnvoll ist.
Für die barometrische Höhenformel gilt dann:
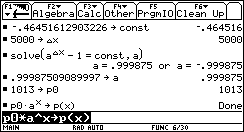
Mit ![]() ® w ® y1(x)=
p(x) und
® w ® y1(x)=
p(x) und ![]() ® r erhält man folgende Graphen:
® r erhält man folgende Graphen:
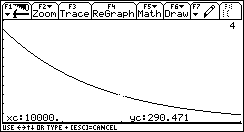 |
 |
|
|
|
 |
 |
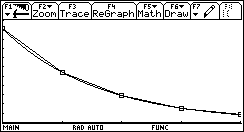
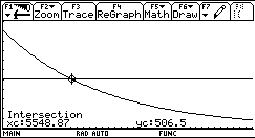
Um die Halbwertshöhe, also jene Höhe, in der der ursprüngliche
Druck um die Hälfte abgefallen ist, zu bestimmen definiert man im
Y=Editor die konstante Funktion ![]() .
Die x-Koordinate des Schnittpunktes der konstanten Funktion mit der Exponentialfunktion
ergibt dann die Halbwertshöhe.
.
Die x-Koordinate des Schnittpunktes der konstanten Funktion mit der Exponentialfunktion
ergibt dann die Halbwertshöhe.
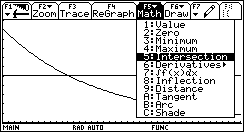
Mit ![]() ® 5 können Schnittpunkte bestimmt werden.
Dabei wird man aufgefordert zunächst die beiden Graphen auszuwählen,
danach muss der Schnittpunkt noch eingegrenzt werden, indem man eine untere
und obere Grenze für den x-Wert angibt (Wichtig, für den Fall,
das mehr als ein Schnittpunkt vorhanden ist).
® 5 können Schnittpunkte bestimmt werden.
Dabei wird man aufgefordert zunächst die beiden Graphen auszuwählen,
danach muss der Schnittpunkt noch eingegrenzt werden, indem man eine untere
und obere Grenze für den x-Wert angibt (Wichtig, für den Fall,
das mehr als ein Schnittpunkt vorhanden ist).
 |
 |
oder ![]()
Formt man jedoch die Gleichung mit Hilfe der Potenzgesetze geeignet um, so lässt sich auch diese Gleichung ohne Zuhilfenahme des Logarithmus lösen.
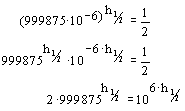
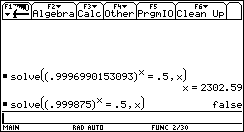 |
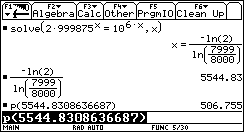 |
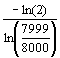 .
Hier kann man schon auf den Logarithmus als Umkehrfunktion der Exponentialfunktion
hinweisen. Den approximierten Wert für
.
Hier kann man schon auf den Logarithmus als Umkehrfunktion der Exponentialfunktion
hinweisen. Den approximierten Wert für Gerald KAISER , HTBL Kapfenberg
| Einsatz moderner Hilfsmittel im Mathematikunterricht |
Der Schüler ist mit dem Begriff der Potenzreihe vertraut. Er weiß, dass sich eine konvergente Potenzreihe wie eine Funktion verhält. Man kann sie unter anderem gliedweise differenzieren und die Potenzreihe einer Funktion ist eindeutig.
Wählt man den Entwicklungspunkt x0 = 0, so ergibt sich
die Darstellung
f(x) =![]() =
= ![]() mit
(
mit
( ![]() )
.
)
.
1. Wie kann man eine Funktion in eine Potenzreihe entwickeln?
Die Funktion sinx soll an der Stelle x0 = 0 in eine Potenzreihe
entwickelt werden.
Wie kann man die Koeffizienten an bestimmen?
sinx = ![]()
Setzt man für x = 0 in die Gleichung ein, so erhält man den Koeffizienten a0. Da man eine Potenzreihe gliedweise differenzieren kann, ist die Ermittlung der weiteren Koeffizienten kein Problem mehr. Mit dem TI 92 soll dies nun mechanisiert werden.
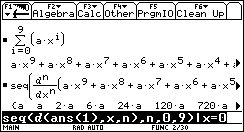 |
Wir geben zunächst die rechte Seite bis zur 9.Potenz ein. Für die Ermittlung der Koeffizienten ai schreibt man sie zunächst als Konstanten a an. Danach bildet man die ersten 9 Ableitungen mit Hilfe des Sequence-Befehles und setzen x = 0, wobei für n = 0 der Funktionswert an der Stelle x = 0 ermittelt wird. |
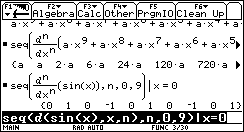 |
Nun ermittelt man den Funktionswert und die Ableitungswerte von sinx an der Stelle x = 0. |
Im nächsten Schritt ermittelt man die Koeffizienten ai.
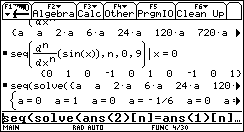 |
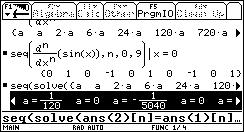 |
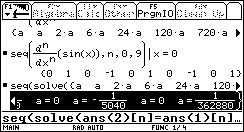 |
Dazu setzt man die Liste der einzelnen Ableitungen
der Polynome am Entwicklungspunkt x = 0 mit der Liste der Ableitungen von
sin x gleich und lösen die Gleichungen nach a auf.
|
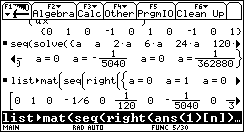 |
Man wandelt die Liste in einen Vektor um. Durch Verwendung von right im Befehl erhält man nur die Zahlenwerte der Koeffizienten. Alle Koeffizienten mit geradem Index sind dabei null. |
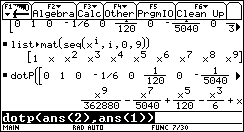 |
Zur Ermittlung der Potenzreihe bildet man zunächst die Folge mit den Potenzen der Variablen x und wandelt diese wiederum in einen Vektor um. Abschließend bildet man das Skalarprodukt der beiden Vektoren und erhält die Potenzreihe. |
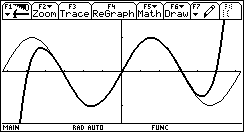 |
Graphische Darstellung der Potenzreihe und der Funktion sinx. |
Abschließend erfolgt die Bemerkung, dass diese Potenzreihe die allgemeine Form der Taylor-Reihe ( Mac Laurin-Reihe) darstellt. Es wird nun die Formel für die Taylor-Reihe erarbeitet.
2. Approximation der Funktion y = sinx durch Taylorpolynome
Der Schüler kennt die Formel für die Taylor-Reihe. Er hat
händisch Funktionen in Taylorpolynome entwickelt. Dabei werden Tabellen
für die Taylorpolynome erstellt und graphisch dargestellt.
Die nächste Frage stellt sich sofort. In welchem Bereich kann
eine Funktion durch eine Potenzreihe angenähert werden?
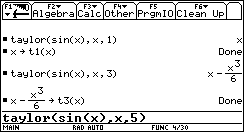
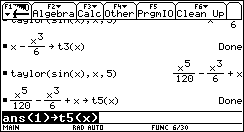
Nun verwendet man den vordefinierten Befehl für die Taylor-Reihe
und ermittelt 3 Taylor-polynome.
 |
 |
 |
 |
Wir wollen nun den Bereich ermitteln, indem die Abweichung der Funktion
sinx vom Taylorpolynom höchstens 1% beträgt. Die dabei entstehenden
Gleichungen werden mit dem TI 92 gelöst.
 |
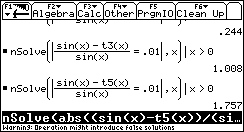 |
Es ergeben sich für
Zum Abschluss stellen wir die Funktion sinx und die 3 Taylorpolynome in Tabellenform dar. Dabei wählen wir eine Schrittweite von 0,1 rad.t1(x) :rad ( 14,0°)
t3(x) :rad ( 57,7°)
t5(x):rad (101,0°)
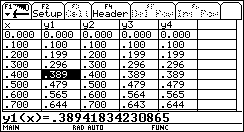 |
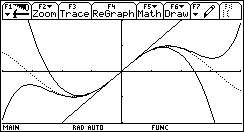
y1(x) = sinx,
y2(x) = t1(x), y3(x) = t3(x), y4(x) = t5(x) |