Peter Weilharter, HTBLuVA Mödling

Mathematische Inhalte:

Genauigkeitsbetrachtungen, Konditionsproblematik

Anwendung:

Kurzzusammenfassung:

Zeitaufwand:

Mediales Umfeld:

Viele Berechnungen führen auf die Wahl von bestimmten Ausgangswerten zurück, die je nach Aufgabenstellung besonders gut bzw. auch schlecht gewählt werden können. Schon die kleinsten Abweichungen vom Anfangswert können zu ganz verschiedenen Ergebnissen, oder im Extremfall zu gar keinem Ergebnis führen.

Diese Problematik nennt man Konditionierung.

Eine empfindliche Abhängigkeit der Lösungswerte von den Angaben erfordert daher immer eine genau Überprüfung der numerischen Lösung.

 2. Der Schmetterlingseffekt

"Moderne Wettermodelle arbeiten mit einem Netzwerk von Punkten im maßstabsverkleinerten Abstand von sechzig Meilen; doch selbst dann noch müssen mehrere Ausgangsdaten als Schätzwerte eingesetzt werden, denn Bodensituation und Satelliten können nicht alles erfassen. Aber nehmen wir einmal an, die Erdoberfläche sei mit Sensoren bedeckt, die etwa einen halben Meter voneinander entfernt lägen und in diesem Abstand bis in die höchsten Lagen der Erdathmosphäre reichten. Nehmen wir ferner an, jeder dieser Sensoren liefere absolut präzise Daten bezüglich Temperatur, Luftdruck, Luftfeuchtigkeit und jedes anderen Wetterfaktors, den ein Meterologe sich nur wünschen kann. Nun sollten genau zur Mittagszeit all diese Daten in einen unbegrenzt leistungsfähigen Computer gespeichert werden, und dieser würde dann berechnen, was an jedem Punkt der Welt um 12.01, dann um 12.02, danach um 12.03 geschehen würde....

Selbst dieser Computer wäre nicht imstande, eine Voraussage darüber zu treffen, ob es in Princetown / New Jersey an irgendeinem Tag einen Monat später regnen oder die Sonne scheinen würde. Bereits am Mittag würden die Zwischenräume der Sensoren Schwankungen verdecken, die der Computer nicht vorausberechnen konnte: geringfügige Abweichungen von den Durchschnittswerten. Um 12.01 hätten diese Abweichungen bei dem einen halben Meter weiter entfernten Sensor bereits zu geringfügigen Berechnungsfehlern geführt.

Bald aber würden diese Fehler sich in der Größenordnung von fünf Metern vervielfältigt haben und schließlich zu Weltmaßstäben anwachsen." (J.Cleick, Chaos – die Ordnung des Universums)

Dieses Phänomen wurde als Schmetterlingseffekt bekannt, nach dem Titel eines Aufsatzes von Edward N. Lorenz "Kann der Flügelschlag eines Schmetterlings in Brasilien einen Tornado in Texas hervorrufen?". Fortschrittliche Rechenqualitätskontrolle beim Wetterbericht bedeutet, beurteilen zu können, ob sich die Mechanismen im Kern der Wetterbildung augenblicklich in einem stabilen oder instabilen Zustand befinden.

3. NEWTONsches Näherungsverfahren zur Lösung von Gleichungen höheren Grades

Die Lösungen einer quadratischen Gleichung können algebraisch beliebig genau berechnet werden. Der zeichnerische Weg liefert nur mäßig genaue Werte.

Die algebraische Lösung von Gleichungen 3.Grades erfordert eine umfangreiche Rechenarbeit; auch das zeichnerische Verfahren ist recht umständlich und ergibt nur angenäherte Werte.

Für Gleichungen von noch höheren Grade kommt im allgemeinen allein die zeichnerische Lösung in Frage. Wegen der geringen Genauigkeit muß man die abgelesenen Nullstellenwerte korrigieren können. Ein Verfahren hierfür stammt von Newton.

Soll eine Nullstelle der Funktion y = f(x) ermittelt werden, und ist x₀ ein in der Nähe der Nullstelle liegender Wert, so ist

ein besserer Näherungswert für die Nullstelle.

Durch wiederholte Anwendung der Formel kann jede gewünschte Annäherung an die Nullstelle erreicht werden.

Um die Auswirkungen der Wahl des Anfangswertes x₀ genauer betrachten zu können, wählen wir als Beispiel die Gleichung:

Funktion:

1.Ableitung:

Ohne Kenntnis vom Graphen und den Funktionswerten der Funktion steht uns die Wahl des Anfangswertes frei. Wir wählen zum Beispiel x₀ = -1.

Mit Hilfe von Excel ergibt sich dann für die Näherungswerte der Nullstelle:

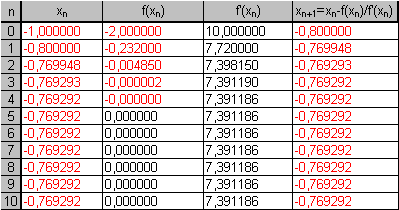
Nach vier Iterationen erhalten wir einen sehr genauen Wert für eine Nullstelle der Gleichung.

Wählen wir aber einen anderen Startwert, z.B. x₀ = 2,870, so erhalten wir:

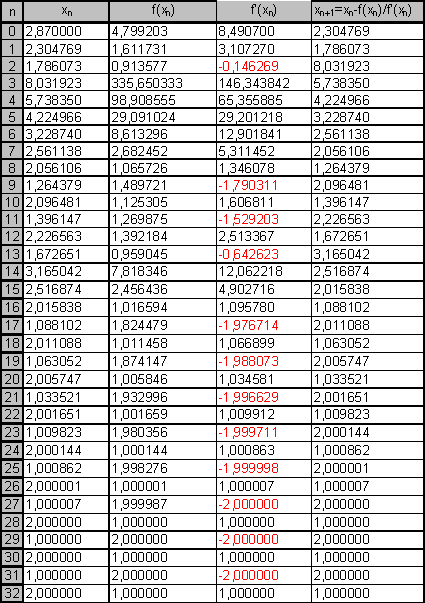
Die Näherungswerte für die gesuchte Nullstelle springen wild durcheinander und pendeln sich schließlich auf zwei Werte 1 und 2 ein. Wie wir oben gesehen haben, ist weder 1 noch 2 eine Nullstelle der obigen Gleichung. Offensichtlich führt nicht jeder beliebige Ausgangswert zu einem vernünftigen Ergebnis. Der Anfangswert war schlecht konditioniert (von seiner Veranlagung her falsch).

Ändern wir nun den Wert um ein Tausendstel auf 2,871 sehen die Näherungswert ganz anders aus:

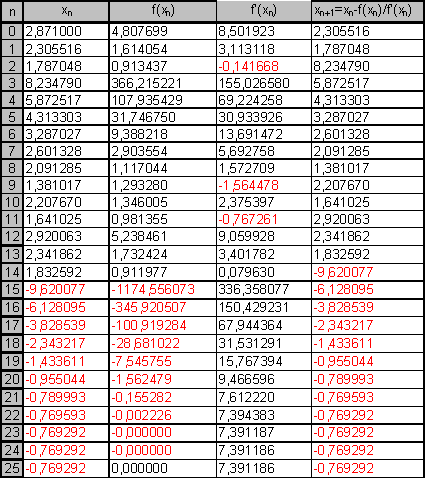
 Nach der dreiundzwanzigsten Iteration erhalten wir wieder unsere gesuchte Nullstelle .

Aus diesem Beispiel geht hervor, wie wichtig es ist den Ausgangspunkt richtig zu wählen. Ein unglücklich gewählter erster Wert kann zu einer uferlosen Rechnerei führen.

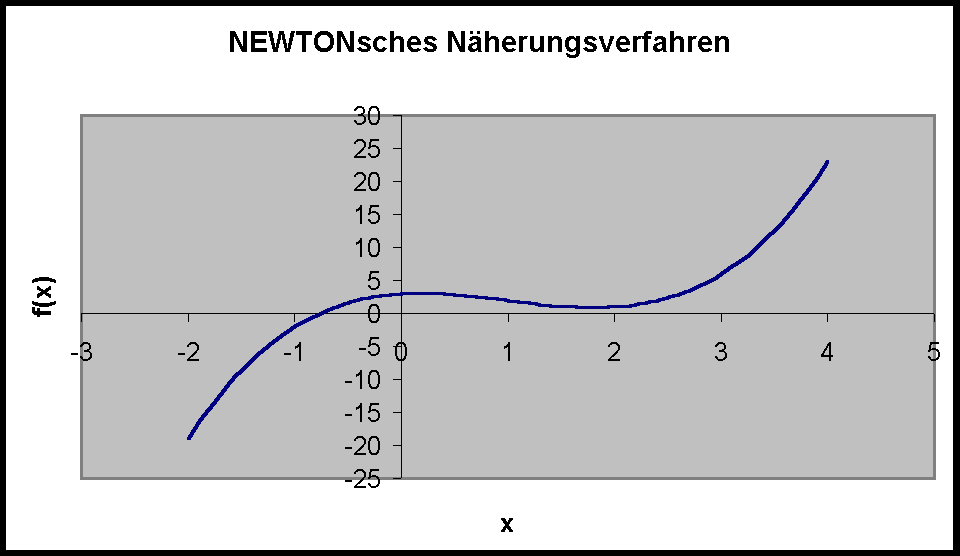
Empfehlenswert ist dabei, daß man sich eine Skizze des Graphen oder eine Wertetabelle anlegt und den Startwert in der Nähe der gesuchten Nullstelle wählt.

Aus der Wertetabelle erkennen wir, daß es eine Nullstelle im Intervall [-1;0] geben muß, da f(-1)<0 (also unterhalb der x-Achse liegt)und f(0)>0 (oberhalb der x-Achse liegt) ist. In der Regel ist es ausreichend wenn man einen der beiden Intervallgrenzen als Startpunkt für x₀ wählt.

Bei der graphischen Lösung würden Werte zwischen –1 und –0,5 in Frage kommen.

4. Genauigkeitsprobleme bei linearen Gleichungssystemen

Ausgangspunkt ist ein lineares Gleichungssystem

 I: x + 2 y = 3

II:0,499 x + 1,001 y = 1,5

Als Schnittpunkt beider Geraden erhalten wir S (1;1).

Nehmen wir nun an, jemand ersetzt den Koeffizienten 1,001 in der zweiten Gleichung durch 1, was hier nur eine kleine Ungenauigkeit bedeutet:

I: x + 2 y = 3

II: 0,499 x + 1 y = 1,5

Als Lösung dieses Gleichungssystems erhalten wir jetzt: x = 0 und y = 1,5.

Die kleine Ungenauigkeit (Eintausendstel!) führt zu einer großen Ungenauigkeit im Ergebnis!

Geometrisch wird dieses Gleichungssystem durch zwei Geraden veranschaulicht, die einander unter einem sehr kleinen Winkel schneiden; es entsteht ein schleifender Schnitt. In einem solche Fall wirkt sich eine kleine Änderung der Geradensteigung wesentlich auf den Schnittpunkt aus.

Gleichungssysteme wie in diesem Beispiel heißen schlecht konditioniert.

Es empfiehlt sich Rechnungen stets genau und auch mit der vollen Taschenrechnergenauigkeit zu führen.

5. Beispiel für schlechte Konditionierung beim Autofahren

 Wie jedem Autofahrer bekannt ist, verhalten sich Autos in geradliniger Vorwärtsbewegung auf ebener Fahrbahn stabil. Es sind nur gelegentliche, geringfügige Lenkradbewegungen erforderlich, um Abweichungen von der Geradeausfahrt zu korrigieren, wie sie z.B: durch Bodenunebenheiten, Seitenwind und anderem hervorgerufen werden. Bei der Rückwärtsfahrt ist die Situation völlig anders. Es sind häufige und größere Lenkradbewegungen notwendig. Verglichen mit der Vorwärtsfahrt liegt offenbar ein instabiler Vorgang vor (schlechte Konditionierung).

Wir verwenden zum Rechnen ein extrem vereinfachtes Modell:

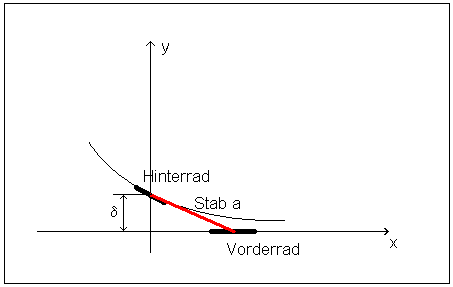
Das gelenkte Vorderrad V ist mit dem ungelenkten Hinterrad H durch einen Stab der Länge a verbunden. V wird längs der x-Achse geführt. Wir betrachten die Bewegung von H, nachdem es durch eine Störung um d aus der x-Achse versetzt wurde. H bewegt sich auf einer sogenannten Schleppkurve (Traktrix), einer Lösung der Differentialgleichung

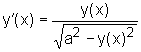
Beispiel: a = 3m, d = 1 cm